Given a m * n matrix mat and an integer K, return a matrix answer where each answer[i][j] is the sum of all elements mat[r][c] for i – K <= r <= i + K, j – K <= c <= j + K, and (r, c) is a valid position in the matrix.

Example 1:
Input: mat = [[1,2,3],[4,5,6],[7,8,9]], K = 1
Output: [[12,21,16],[27,45,33],[24,39,28]]

Example 2:
Input: mat = [[1,2,3],[4,5,6],[7,8,9]], K = 2
Output: [[45,45,45],[45,45,45],[45,45,45]]

Constraints:
m == mat.length
n == mat[i].length
1 <= m, n, K <= 100
1 <= mat[i][j] <= 100

Hints:
How to calculate the required sum for a cell (i,j) fast ?
Use the concept of cumulative sum array.
Create a cumulative sum matrix where dp[i][j] is the sum of all cells in the rectangle from (0,0) to (i,j), use inclusion-exclusion idea.

Matrix Block Sum using Dyanmic Programming Algorithm

We can do this in most straighforward solution. We compute the region of the blocks i.e. top-left corner and bottom-right corner, then we apply another loop to compute the sum of the block. This will be O(R^2.C^2) where R is the rows and C is the columns of the matrix.

We can use the Dynamic Programming Algorithm to store the partial prefix sum of the matrix in i.e. DP array. This will take O(RC) to compute and O(RC) space requirement is needed. Then as we iterate again the coordinate of the matrix, we compute the two corners of the block. Then we can use the prefix sum in the DP array to compute the sum of the block.

Sum of Block for the Matrix from top-left corner [a][b] to bottom-right [c][d] is equal to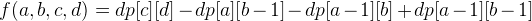

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int K) {
        int row = mat.size();
        if (row == 0) return {{}};
        int col = mat[0].size();
        vector<vector<int>> res(row, vector<int>(col, 0));
        vector<vector<int>> dp(row, vector<int>(col, 0));
        // store the sum in dp[r][c] where the sum from [0, 0] to [r, c] is computed.
        for (int r = 0; r < row; ++ r) {
            for (int c = 0; c < col; ++ c) {
                int sum = mat[r][c];
                if (c > 0) sum += dp[r][c - 1];
                if (r > 0) sum += dp[r - 1][c];
                if ((r > 0) && (c > 0)) sum -= dp[r - 1][c - 1];
                dp[r][c] = sum;
            }
        }
        for (int r = 0; r < row; ++ r) {
            for (int c = 0; c < col; ++ c) {
                int minr = max(0, r - K);
                int minc = max(0, c - K) ;
                int maxr = min(r + K, row - 1);
                int maxc = min(c + K, col - 1);
                if (minr > 0 && minc > 0) {
                    res[r][c] = dp[maxr][maxc] + dp[minr - 1][minc - 1] - 
                        dp[minr - 1][maxc] - dp[maxr][minc - 1];
                } else if (minr > 0) {
                    res[r][c] = dp[maxr][maxc] - dp[minr - 1][maxc]; 
                } else if (minc > 0) {
                    res[r][c] = dp[maxr][maxc] - dp[maxr][minc - 1];                    
                } else {
                    res[r][c] = dp[maxr][maxc];
                }
            }
        }        
        return res;
    }
};

class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int K) {
        int row = mat.size();
        if (row == 0) return {{}};
        int col = mat[0].size();
        vector<vector<int>> res(row, vector<int>(col, 0));
        vector<vector<int>> dp(row, vector<int>(col, 0));
        // store the sum in dp[r][c] where the sum from [0, 0] to [r, c] is computed.
        for (int r = 0; r < row; ++ r) {
            for (int c = 0; c < col; ++ c) {
                int sum = mat[r][c];
                if (c > 0) sum += dp[r][c - 1];
                if (r > 0) sum += dp[r - 1][c];
                if ((r > 0) && (c > 0)) sum -= dp[r - 1][c - 1];
                dp[r][c] = sum;
            }
        }
        for (int r = 0; r < row; ++ r) {
            for (int c = 0; c < col; ++ c) {
                int minr = max(0, r - K);
                int minc = max(0, c - K) ;
                int maxr = min(r + K, row - 1);
                int maxc = min(c + K, col - 1);
                if (minr > 0 && minc > 0) {
                    res[r][c] = dp[maxr][maxc] + dp[minr - 1][minc - 1] - 
                        dp[minr - 1][maxc] - dp[maxr][minc - 1];
                } else if (minr > 0) {
                    res[r][c] = dp[maxr][maxc] - dp[minr - 1][maxc]; 
                } else if (minc > 0) {
                    res[r][c] = dp[maxr][maxc] - dp[maxr][minc - 1];                    
                } else {
                    res[r][c] = dp[maxr][maxc];
                }
            }
        }        
        return res;
    }
};

Overall, the algorithmic complexity of the above Dynamic Programming is O(RC).

–EOF (The Ultimate Computing & Technology Blog) —