Given two strings text1 and text2, return the length of their longest common subsequence.

A subsequence of a string is a new string generated from the original string with some characters(can be none) deleted without changing the relative order of the remaining characters. (eg, “ace” is a subsequence of “abcde” while “aec” is not). A common subsequence of two strings is a subsequence that is common to both strings.

If there is no common subsequence, return 0.

Example 1:
Input: text1 = “abcde”, text2 = “ace”
Output: 3
Explanation: The longest common subsequence is “ace” and its length is 3.

Example 2:
Input: text1 = “abc”, text2 = “abc”
Output: 3
Explanation: The longest common subsequence is “abc” and its length is 3.

Example 3:
Input: text1 = “abc”, text2 = “def”
Output: 0
Explanation: There is no such common subsequence, so the result is 0.

Constraints:
1 <= text1.length <= 1000
1 <= text2.length <= 1000
The input strings consist of lowercase English characters only.

Hints:
Try dynamic programming. DP[i][j] represents the longest common subsequence of text1[0 … i] & text2[0 … j].
DP[i][j] = DP[i – 1][j – 1] + 1 , if text1[i] == text2[j] DP[i][j] = max(DP[i – 1][j], DP[i][j – 1]) , otherwise

Longest Common Subsequence using Dynamic Programming Algorithm

Sure, we can bruteforce, try to find all the common subsequence from both strings, and compare if they match. But the complexity is so high that it won’t be practical.

One better solution is to use the dynamic programming algorithm where we use a two dimensional array dp[i][j] to store the maximum length of the common subsequence from s1[0..i] and s2[0..j].

Then, a O(N^2) qudaric loop is needed, if we have s1[i] == s2[j], we update the answer to dp[i-1][j-1], otherwise, it is the maximum of dp[i-1][j] and dp[i][j-1].

The DP formula is:

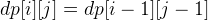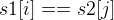
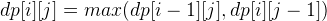if
if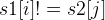

By implementing the above equations, we have the following C++ code.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int len1 = text1.size();
        int len2 = text2.size();
        vector<vector<int>> dp(len1, vector<int>(len2, 0));
        dp[0][0] = text1[0] == text2[0] ? 1 : 0;
        for (int i = 0; i < len1; ++ i) {
            for (int j = 0; j < len2; ++ j) {
                if (text1[i] == text2[j]) {
                    if ((i > 0) && (j > 0)) {
                        dp[i][j] = dp[i - 1][j - 1] + 1;
                    } else {
                        dp[i][j] = 1;
                    }
                } else {
                    if (i > 0) dp[i][j] = max(dp[i][j], dp[i - 1][j]);
                    if (j > 0) dp[i][j] = max(dp[i][j], dp[i][j - 1]);
                }
            }
        }
        return dp.back().back();
    }
};

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int len1 = text1.size();
        int len2 = text2.size();
        vector<vector<int>> dp(len1, vector<int>(len2, 0));
        dp[0][0] = text1[0] == text2[0] ? 1 : 0;
        for (int i = 0; i < len1; ++ i) {
            for (int j = 0; j < len2; ++ j) {
                if (text1[i] == text2[j]) {
                    if ((i > 0) && (j > 0)) {
                        dp[i][j] = dp[i - 1][j - 1] + 1;
                    } else {
                        dp[i][j] = 1;
                    }
                } else {
                    if (i > 0) dp[i][j] = max(dp[i][j], dp[i - 1][j]);
                    if (j > 0) dp[i][j] = max(dp[i][j], dp[i][j - 1]);
                }
            }
        }
        return dp.back().back();
    }
};

If we slightly increase the DP array by one, and update dp[i+1][j+1], we have a cleaner code.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int n1 = text1.size(), n2 = text2.size();
        vector<vector<int>> dp(n1 + 1, vector<int>(n2 + 1));
        for (int i = 0; i < n1; ++ i) {
            for (int j = 0; j < n2; ++ j) {
                if (text1[i] == text2[j]) {
                    dp[i + 1][j + 1] = dp[i][j] + 1;
                } else {
                    dp[i + 1][j + 1] = max(dp[i + 1][j], dp[i][j + 1]);
                }
            }            
        }
        return dp[n1][n2];
    }
};

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int n1 = text1.size(), n2 = text2.size();
        vector<vector<int>> dp(n1 + 1, vector<int>(n2 + 1));
        for (int i = 0; i < n1; ++ i) {
            for (int j = 0; j < n2; ++ j) {
                if (text1[i] == text2[j]) {
                    dp[i + 1][j + 1] = dp[i][j] + 1;
                } else {
                    dp[i + 1][j + 1] = max(dp[i + 1][j], dp[i][j + 1]);
                }
            }            
        }
        return dp[n1][n2];
    }
};

Both implementations are having O(N^2) time and space complexity.

–EOF (The Ultimate Computing & Technology Blog) —