A complete binary tree is a binary tree that each level except possibiliy the last level, is completed filled. Suppose you are giving a binary tree represented as an array. For example, [3, 6, 2, 9, -1, 10] retpresents the following binary tree, where -1 indicates it is a NULL node.

    3
  6   2
9    10

Write a function that determines whether the left or right branch of the tree is larger. The size of each branch is the sum of the node vlaues. The function should return the string “Right” if the right side is larger and “Left” if the left side is larger. If the tree has zero nodes or if the size of the branches are equal, an empty string “” should be returned.

How to Store/Index a Complete Binary Tree?

We can use an array to index/store a complete binary tree where the root index starts at ONE, and the left child index is always twice its parent index, and the right index is the twice parent index plus one.

For example, in above complete binary tree, the Node 6 has index 2 which is equal to 2*ROOT = 2 * 1. and the Node 2 is 2*ROOT+1 = 2*1+1 = 3.

In the following Javascript method, we have inlined local recursive method that takes the array (complete binary tree) and a node index, which will recursively sum up the nodes in the branch until it gets to the leave nodes.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

const solution = (arr) => {
    if (!arr) return "";
    if (arr.length === 0) return "";    
    const sum = (arr, idx) => {
        if (idx - 1 < arr.length) {
            if (arr[idx - 1] === -1) return 0;
            return arr[idx - 1] + sum(arr, idx * 2) + sum(arr, idx * 2 + 1);
        }
        return 0;
    };
    const left = sum(arr, 2);
    const right = sum(arr, 3);
    return (left == right) ? "" : (left > right ? "Left" : "Right");
};

const solution = (arr) => {
    if (!arr) return "";
    if (arr.length === 0) return "";    
    const sum = (arr, idx) => {
        if (idx - 1 < arr.length) {
            if (arr[idx - 1] === -1) return 0;
            return arr[idx - 1] + sum(arr, idx * 2) + sum(arr, idx * 2 + 1);
        }
        return 0;
    };
    const left = sum(arr, 2);
    const right = sum(arr, 3);
    return (left == right) ? "" : (left > right ? "Left" : "Right");
};

Then we can simply call the function twice to compute the sum for left and right branch respectively. The time complexity is O(N) where N is the number of the nodes in the complete binary tree. And the space complexity is O(logN) because the recursion implies a call stack, and the depth for a complete binary tree is O(logN).

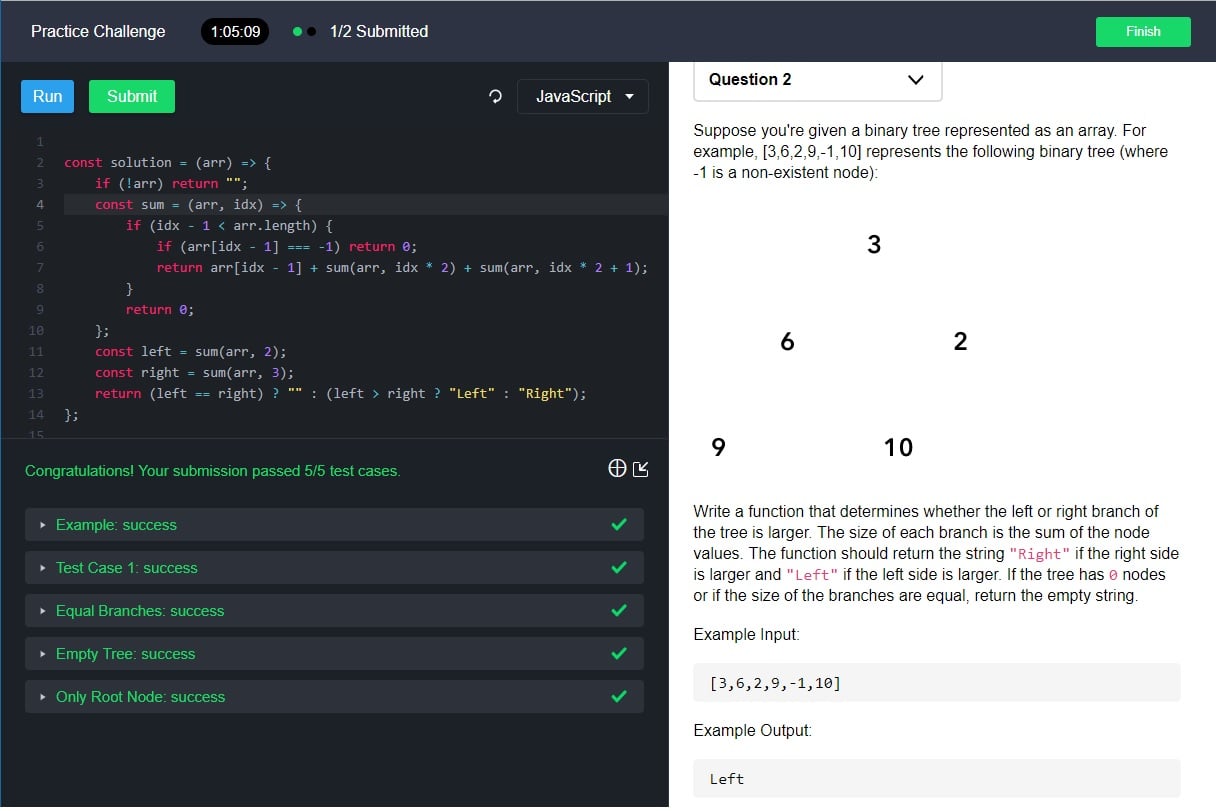
binary-tree-left-sum-or-right-sum-larger

You can practice this problem at Hired.com which is a nice career platform for programmers.

–EOF (The Ultimate Computing & Technology Blog) —