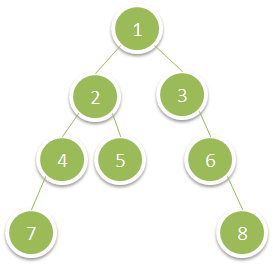
Compute the Deepest Leaves Sum of a Binary Tree using BFS or DFS

  • 时间：2020-09-12 10:17:13
  • 分类：网络文摘
  • 阅读：102 次

Given a binary tree, return the sum of values of its deepest leaves.

Example 1:
Input: root = [1,2,3,4,5,null,6,7,null,null,null,null,8]
Output: 15

binary-tree Compute the Deepest Leaves Sum of a Binary Tree using BFS or DFS Algorithms algorithms BFS c / c++ DFS

binary-tree

Constraints:
The number of nodes in the tree is between 1 and 10^4.
The value of nodes is between 1 and 100.

We can traversal the binary tree using level-by-level namely Breadth First Search algorithm or depth first search.

Breadth First Search Algorithm to Compute the Deepest Leaves Sum of a Binary Tree

We can expand all the nodes in the same level by sum up on those. However, we need to reset the sum to zero when expanding a new level, then the last sum would be the answer we are looking for.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        if (!root) return 0;
        queue<TreeNode*> Q;
        Q.push(root);
        int sum;
        while (!Q.empty()) {
            sum = 0;  // reset the sum for a new level
            int curSize = Q.size();
            for (int i = 0; i < curSize; ++ i) {
                auto p = Q.front();
                sum += p->val;
                Q.pop();
                if (p->left) {
                    Q.push(p->left);
                }
                if (p->right) {
                    Q.push(p->right);
                }
            }
        }
        return sum;
    }
};
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        if (!root) return 0;
        queue<TreeNode*> Q;
        Q.push(root);
        int sum;
        while (!Q.empty()) {
            sum = 0;  // reset the sum for a new level
            int curSize = Q.size();
            for (int i = 0; i < curSize; ++ i) {
                auto p = Q.front();
                sum += p->val;
                Q.pop();
                if (p->left) {
                    Q.push(p->left);
                }
                if (p->right) {
                    Q.push(p->right);
                }
            }
        }
        return sum;
    }
};

The time complexity is O(N) and the space requirement is also O(N) where N is the number of the nodes in the binary tree.

How to Compute the Deepest Leaves Sum of a Binary Tree using Depth First Search Algorithms

We can store the node values in a hash map either unordered_map or map where the key is the depth and the value is the vector of the values. At the same time, we keep track of the maximum depth we’ve visited.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        helper(root, 0);
        int sum = 0;
        for (const auto &n: data[curMax]) {
            sum += n;
        }
        return sum;
    }
private:
    unordered_map<int, vector<int>> data;
    int curMax = -1;
    void helper(TreeNode* root, int depth) {
        if (root == nullptr) return;        
        curMax = max(curMax, depth);
        data[depth].push_back(root->val);
        helper(root->left, depth + 1);
        helper(root->right, depth + 1);
    }
};
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        helper(root, 0);
        int sum = 0;
        for (const auto &n: data[curMax]) {
            sum += n;
        }
        return sum;
    }
private:
    unordered_map<int, vector<int>> data;
    int curMax = -1;
    void helper(TreeNode* root, int depth) {
        if (root == nullptr) return;        
        curMax = max(curMax, depth);
        data[depth].push_back(root->val);
        helper(root->left, depth + 1);
        helper(root->right, depth + 1);
    }
};

The C++ map sorts the keys by default, meaning that we can use the rbegin() or –end() to get the maximum key for the map. This simplifies the implementation. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        helper(root, 0);
        int sum = 0;
        for (const auto &n: data.rbegin()->second) {
            sum += n;
        }
        return sum;
    }
private:
    map<int, vector<int>> data;
    void helper(TreeNode* root, int depth) {
        if (root == nullptr) return;        
        data[depth].push_back(root->val);
        helper(root->left, depth + 1);
        helper(root->right, depth + 1);
    }
};
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        helper(root, 0);
        int sum = 0;
        for (const auto &n: data.rbegin()->second) {
            sum += n;
        }
        return sum;
    }
private:
    map<int, vector<int>> data;
    void helper(TreeNode* root, int depth) {
        if (root == nullptr) return;        
        data[depth].push_back(root->val);
        helper(root->left, depth + 1);
        helper(root->right, depth + 1);
    }
};

The above DFS implementations have O(N) space requirement (usage of std::map or std::unordered_map), and O(N) time where N is the number of nodes to visit.

Another solution would be to compute the depth of the binary tree first, then compute the sum only for the maximum depth. Both DFS are implemented in Recursion. The sum will be accumulated only when we reach the depth. N nodes will be visited twice.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        if (!root) return 0;
        int depth = getDepth(root);
        return getSumAt(root, depth);
    }
private:
    int getDepth(TreeNode* root) {
        if (root == NULL) return 0;
        return max(getDepth(root->left), getDepth(root->right)) + 1;
    }
    int getSumAt(TreeNode* root, int depth) {
        if (root == NULL) return 0;
        if (depth == 1) return root->val;
        return getSumAt(root->left, depth - 1) + 
            getSumAt(root->right, depth - 1);
    }
};
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        if (!root) return 0;
        int depth = getDepth(root);
        return getSumAt(root, depth);
    }
private:
    int getDepth(TreeNode* root) {
        if (root == NULL) return 0;
        return max(getDepth(root->left), getDepth(root->right)) + 1;
    }
    int getSumAt(TreeNode* root, int depth) {
        if (root == NULL) return 0;
        if (depth == 1) return root->val;
        return getSumAt(root->left, depth - 1) + 
            getSumAt(root->right, depth - 1);
    }
};

–EOF (The Ultimate Computing & Technology Blog) —

推荐阅读：
How Dedicated Servers Boost the Performance of A Business Blog　 Irish Travel Blogger Visits Every Country In The World, Just In 　 How to Build an Online Store on WordPress Using WooCommerce　 C++ Coding Reference: is_sorted_until() and is_sorted()　 Two Rectangles Overlap Detection Algorithm in C++　 C++ Coding Reference: next_permutation() and prev_permutation()　 C++ Coding Reference: count and count_if　 How to Reorder Data in Log Files using the Custom Sorting Algori　 C++ Coding Reference: std::accumulate() and examples　 C++ Coding Reference: sort() and stable_sort()　
评论列表
添加评论