Return the root node of a binary search tree that matches the given preorder traversal.

(Recall that a binary search tree is a binary tree where for every node, any descendant of node.left has a value < node.val, and any descendant of node.right has a value > node.val. Also recall that a preorder traversal displays the value of the node first, then traverses node.left, then traverses node.right.)

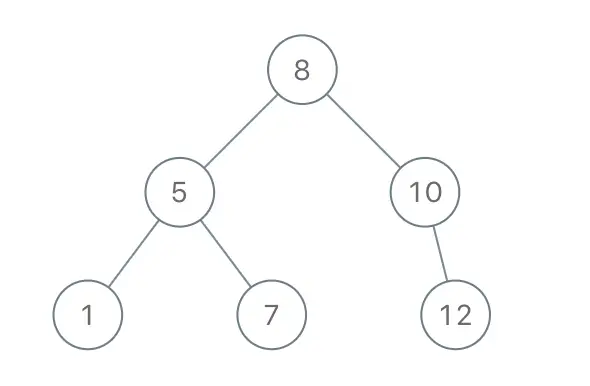
Input: [8,5,1,7,10,12]

Binary Search Tree

Output: [8,5,10,1,7,null,12]

Note:
1 <= preorder.length <= 100
The values of preorder are distinct.

Construct Binary Search Tree Algorithm from Preorder

The first element in the preorder traversal is the root node, and its left elements are always smaller than its value and the right elements are larger.

Therefore, we can find the index where the value is bigger than the root, thus separating the left and right nodes.

Recursively, we can construct the binary search tree by finding the pivot index.

The following C++ implementation uses a helper function which adds two parameter i.e. left and right index forming current sub-tree.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* bstFromPreorder(vector<int>& preorder) {
        return helper(preorder, 0, preorder.size() - 1);
    }
    
    TreeNode* helper(vector<int>& preorder, int left, int right) {
        if (left > right) return NULL;
        int root = preorder[left];
        int r = right + 1;
        for (int i = left + 1; i <= right; ++ i) {
            if (preorder[i] >= root) { // find the first of right node
                r = i;
                break;
            }
        }
        TreeNode* rootNode = new TreeNode(root);
        rootNode->left = helper(preorder, left + 1, r - 1);
        rootNode->right = helper(preorder, r, right);
        return rootNode;
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* bstFromPreorder(vector<int>& preorder) {
        return helper(preorder, 0, preorder.size() - 1);
    }
    
    TreeNode* helper(vector<int>& preorder, int left, int right) {
        if (left > right) return NULL;
        int root = preorder[left];
        int r = right + 1;
        for (int i = left + 1; i <= right; ++ i) {
            if (preorder[i] >= root) { // find the first of right node
                r = i;
                break;
            }
        }
        TreeNode* rootNode = new TreeNode(root);
        rootNode->left = helper(preorder, left + 1, r - 1);
        rootNode->right = helper(preorder, r, right);
        return rootNode;
    }
};

The time complexity is O(N) where all nodes need to be visited exactly once and the space complexity is also O(N) where the binary search tree may be degraded into a singly-linked list.

Converting to Java, the following is the Java implementation to construct a binary search tree from a preorder traversal.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode bstFromPreorder(int[] preorder) {
        return helper(preorder, 0, preorder.length - 1);
    }
    
    private TreeNode helper(int[] preorder, int left, int right) {
        if (left > right) return null;
        int root = preorder[left];
        int r = right + 1;
        for (int i = left + 1; i <= right; ++ i) {
            if (preorder[i] >= root) {
                r = i;
                break;
            }
        }
        TreeNode rootNode = new TreeNode(root);
        rootNode.left = helper(preorder, left + 1, r - 1);
        rootNode.right = helper(preorder, r, right);
        return rootNode;
    }    
}

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode bstFromPreorder(int[] preorder) {
        return helper(preorder, 0, preorder.length - 1);
    }
    
    private TreeNode helper(int[] preorder, int left, int right) {
        if (left > right) return null;
        int root = preorder[left];
        int r = right + 1;
        for (int i = left + 1; i <= right; ++ i) {
            if (preorder[i] >= root) {
                r = i;
                break;
            }
        }
        TreeNode rootNode = new TreeNode(root);
        rootNode.left = helper(preorder, left + 1, r - 1);
        rootNode.right = helper(preorder, r, right);
        return rootNode;
    }    
}

We can use Arrays.copyOfRange(oldArray, fromIndex, toIndex) to return a partial copy of the array, thus we don’t need to have the helper function, instead, we can just recursively call the existing method with copies (portion) of the preorder traversal – e.g. of the sub trees.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode bstFromPreorder(int[] preorder) {
        if (preorder == null || preorder.length == 0) return null;
        int root = preorder[0];
        int r = preorder.length;
        for (int i = 1; i < preorder.length; ++ i) {
            if (preorder[i] >= root) {
                r = i;
                break;
            }
        }
        TreeNode rootNode = new TreeNode(root);
        int[] leftTree = null;
        if (r >= 1) {
            leftTree = Arrays.copyOfRange(preorder, 1, r);
        }
        int[] rightTree = Arrays.copyOfRange(preorder, r, preorder.length);
        rootNode.left = bstFromPreorder(leftTree);
        rootNode.right = bstFromPreorder(rightTree);
        return rootNode;
    }
}

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode bstFromPreorder(int[] preorder) {
        if (preorder == null || preorder.length == 0) return null;
        int root = preorder[0];
        int r = preorder.length;
        for (int i = 1; i < preorder.length; ++ i) {
            if (preorder[i] >= root) {
                r = i;
                break;
            }
        }
        TreeNode rootNode = new TreeNode(root);
        int[] leftTree = null;
        if (r >= 1) {
            leftTree = Arrays.copyOfRange(preorder, 1, r);
        }
        int[] rightTree = Arrays.copyOfRange(preorder, r, preorder.length);
        rootNode.left = bstFromPreorder(leftTree);
        rootNode.right = bstFromPreorder(rightTree);
        return rootNode;
    }
}

The Python’s implementation can be found here (using the list comprehension): How to Construct Binary Search Tree from Preorder Traversal in Python?

Related Binary Tree Construction Algorithms

You may also like the following posts on the similar tree problems.

• Recursive Algorithm to Construct Binary Tree from Preorder and Postorder Traversal
• How to Construct Binary Search Tree from Preorder Traversal in Python?
• Algorithm to Construct Binary Tree from Preorder and Inorder Traversal
• How to Construct Binary Search Tree from Preorder Traversal? (C++ and Java)
• How to Construct String from Binary Tree?
• How to Balance a Binary Search Tree using Recursive Inorder Traversal Algorithm?
• How to Construct the Maximum Binary Tree using Divide-and-Conquer Recursion Algorithm?
• How to Construct Binary Tree from Inorder and Postorder Traversal using Depth First Search Algorithm (Recursion)?
• How to Construct Binary Tree from String (Binary Tree Deserialization Algorithm)

–EOF (The Ultimate Computing & Technology Blog) —