For a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees. A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations. Write a function that determines whether two binary trees are flip equivalent. The trees are given by root nodes root1 and root2.

Example 1:
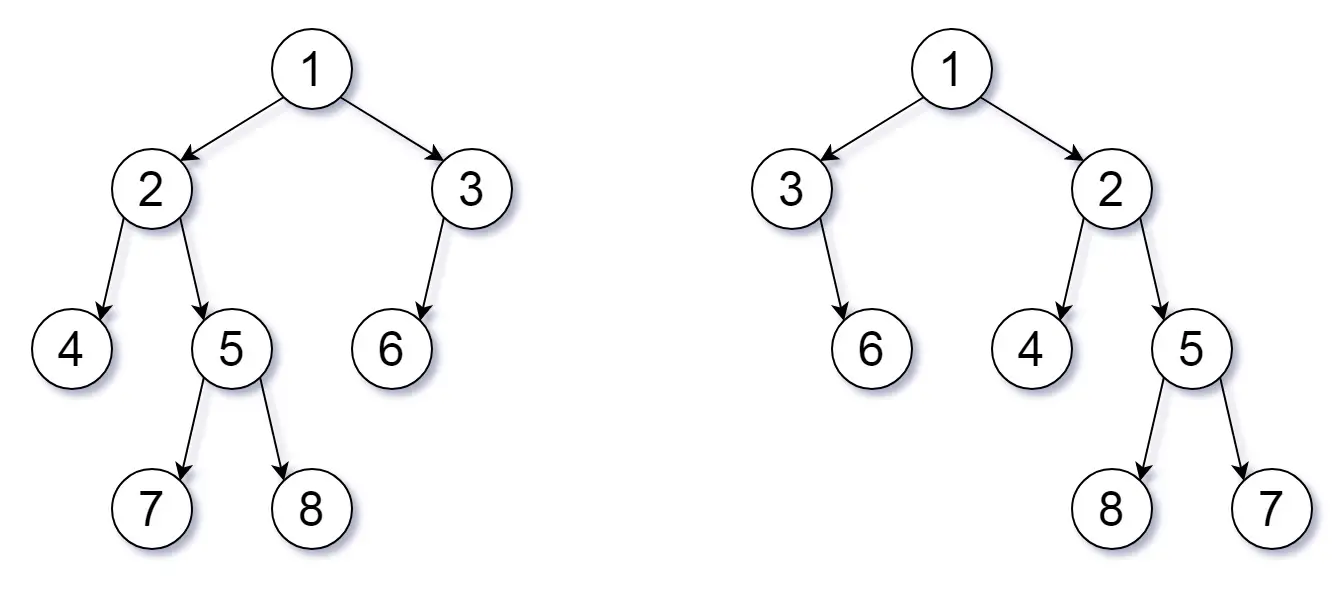
Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
Output: true
Explanation: We flipped at nodes with values 1, 3, and 5.

binary-flip-tree

Note:
Each tree will have at most 100 nodes.
Each value in each tree will be a unique integer in the range [0, 99].

Flip Binary Trees Algorithm using Depth First Search (Recursion)

The following C++ implementation of DFS runs at O(Min(N1, N2)) time complexity and O(Min(H1, H2)) space complexity where N1, N2 are the number of nodes and H1, H2 are the heights/depths of the binary trees.

The recursion defines the basic terminate conditions. If two nodes are both NULL (or they are equal), they are flip-equivalent binary trees. If only one node is NULL (another is not), or the values are not equal, then it is NOT a flip-equivalent binary tree. Otherwise, we recursively check two cases. Either both left sub-trees and both right sub-trees are flip equivalent binary trees, or the left sub tree (of tree 1) is flip equivalent to the right sub tree (of tree 2), and right sub tree (of tree 1) is flip equivalent to the left sub tree (of tree 2).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool flipEquiv(TreeNode* root1, TreeNode* root2) {
        if (root1 == root2) return true; // root1 == NULL && root2 == NULL
        if (root1 == NULL || root2 == NULL || root1->val != root2->val) return false;
        return (flipEquiv(root1->left, root2->left) && flipEquiv(root1->right, root2->right)) ||
            (flipEquiv(root1->left, root2->right) && flipEquiv(root1->right, root2->left));
    }    
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool flipEquiv(TreeNode* root1, TreeNode* root2) {
        if (root1 == root2) return true; // root1 == NULL && root2 == NULL
        if (root1 == NULL || root2 == NULL || root1->val != root2->val) return false;
        return (flipEquiv(root1->left, root2->left) && flipEquiv(root1->right, root2->right)) ||
            (flipEquiv(root1->left, root2->right) && flipEquiv(root1->right, root2->left));
    }    
};

Canonical Traversal using Depth First Search (Recursion)

Another C++ solution (also based on DFS that is implemented in Recursion) is as follows where both trees are walked through using Canonical Traversal order (where the smaller node is visited first). Then we just have to compare the output sequences of both trees.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool flipEquiv(TreeNode* root1, TreeNode* root2) {
        vector<int> r1, r2;
        dfs(root1, r1);
        dfs(root2, r2);
        return same(r1, r2); // check if the order is the same
    }    
    
    void dfs(TreeNode* root, vector<int> &r) {
        if (root != NULL) {
            r.push_back(root->val);
            if (root->left == NULL) {
                dfs(root->right, r);
            } else 
            if (root->right == NULL) {
                dfs(root->left, r);
            } else
            if (root->left->val < root->right->val) {
                dfs(root->left, r);
                dfs(root->right, r);
            } else {
                dfs(root->right, r);
                dfs(root->left, r);                    
            }
            r.push_back(-1); // marks end
        }
    }
    
    bool same(const vector<int> &r1, const vector<int> &r2) {
        if (r1.size() != r2.size()) return false;
        for (int i = 0; i < r1.size(); ++ i) {
            if (r1[i] != r2[i]) return false;
        }
        return true;
    }
};

 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool flipEquiv(TreeNode* root1, TreeNode* root2) {
        vector<int> r1, r2;
        dfs(root1, r1);
        dfs(root2, r2);
        return same(r1, r2); // check if the order is the same
    }    
    
    void dfs(TreeNode* root, vector<int> &r) {
        if (root != NULL) {
            r.push_back(root->val);
            if (root->left == NULL) {
                dfs(root->right, r);
            } else 
            if (root->right == NULL) {
                dfs(root->left, r);
            } else
            if (root->left->val < root->right->val) {
                dfs(root->left, r);
                dfs(root->right, r);
            } else {
                dfs(root->right, r);
                dfs(root->left, r);                    
            }
            r.push_back(-1); // marks end
        }
    }
    
    bool same(const vector<int> &r1, const vector<int> &r2) {
        if (r1.size() != r2.size()) return false;
        for (int i = 0; i < r1.size(); ++ i) {
            if (r1[i] != r2[i]) return false;
        }
        return true;
    }
};

The time complexity is O(N1 + N2 + Min(N1, N2) which is O(N1 + N2) because both trees have to be visited entirely. And the space complexity is O(N1 + N2) as additional space has to be allocated to store the Canonical Traversal sequences for both trees.

–EOF (The Ultimate Computing & Technology Blog) —