Depth First Search Algorithm to Find Leaves of a Binary Tree
- 时间:2020-09-26 22:11:41
- 分类:网络文摘
- 阅读:127 次
Given a binary tree, collect a tree’s nodes as if you were doing this: Collect and remove all leaves, repeat until the tree is empty.
Example:
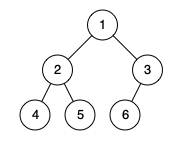
Input: [1,2,3,4,5]1 / \ 2 3 / \ 4 5Output: [[4,5,3],[2],[1]]
Example of a Complete Binary Tree
Explanation:
1. Removing the leaves [4,5,3] would result in this tree:1 / 22. Now removing the leaf [2] would result in this tree:
13. Now removing the leaf [1] would result in the empty tree:
[]
Finding the leaves is easy, but it is not trivial to remove them and iteratively finding new leaves until the tree is empty. We may however simulate the process, which takes time and this requires somehow a complex piece of implementation.
Depth First Search Algorithm to Find the Binary Tree Leaves
We define a function that recursively computes the distances/depth between any nodes to the leaf nodes. Then we can associate the nodes with its depth. This will be implemented using recursion and the following Java code demonstrates the Depth First Search.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | /** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { public List<List<Integer>> findLeaves(TreeNode root) { List<List<Integer>> r = new ArrayList<List<Integer>>(); dfs(root, r); return r; } private int dfs(TreeNode root, List<List<Integer>> r) { if (root == null) return 0; // leave nodes are depth 0. // the depth is the max between two branches + 1 int h = Math.max(dfs(root.left, r), dfs(root.right, r)) + 1; if (r.size() < h) { r.add(new ArrayList<Integer>()); } r.get(h - 1).add(root.val); // put the 'leave' to its level return h; } } |
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<List<Integer>> findLeaves(TreeNode root) {
List<List<Integer>> r = new ArrayList<List<Integer>>();
dfs(root, r);
return r;
}
private int dfs(TreeNode root, List<List<Integer>> r) {
if (root == null) return 0; // leave nodes are depth 0.
// the depth is the max between two branches + 1
int h = Math.max(dfs(root.left, r), dfs(root.right, r)) + 1;
if (r.size() < h) {
r.add(new ArrayList<Integer>());
}
r.get(h - 1).add(root.val); // put the 'leave' to its level
return h;
}
}The DFS runs at O(N) time where N is the number of the nodes in the given binary tree. The space complexity is O(N) as well. The following is the C++ implementation of the same algorithm (so the time and space complexity is the same – O(N)).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: vector<vector<int>> findLeaves(TreeNode* root) { vector<vector<int>> res; dfs(root, res); return res; } int dfs(TreeNode* root, vector<vector<int>> &r) { if (root == NULL) { // leave nodes are depth 0. return 0; } int lv = dfs(root->left, r); int rv = dfs(root->right, r); int h = 1 + max(lv, rv); if (h > r.size()) { r.push_back({}); // allocate for the new level } r[h - 1].push_back(root->val); return h; } }; |
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> findLeaves(TreeNode* root) {
vector<vector<int>> res;
dfs(root, res);
return res;
}
int dfs(TreeNode* root, vector<vector<int>> &r) {
if (root == NULL) { // leave nodes are depth 0.
return 0;
}
int lv = dfs(root->left, r);
int rv = dfs(root->right, r);
int h = 1 + max(lv, rv);
if (h > r.size()) {
r.push_back({}); // allocate for the new level
}
r[h - 1].push_back(root->val);
return h;
}
};The Depth First Search Algorithm is usually implemented using Recursion where a stack will be generated and maintained by the compiler automatically. You could, however, convert the recursion into the iterative approach by manually operating the stack.
–EOF (The Ultimate Computing & Technology Blog) —
推荐阅读:什么是维生素C及维生素C的生理作用 维生素C的测定方法—氧化还原滴定法 哪些人群需要多食用含维生素C的食物 维生素C的主要作用及人体推荐摄入量 补充维生素C的药品维生素C片服用禁忌 维生素C缺乏症的主要表现及其治疗 素食有哪些误区素食者需要注意的问题 素食的分类及适当素食具有的保健作用 冬季咳嗽吃什么自制美味止咳小零食 冬季进补鸡汤要注意 几类人不宜喝鸡汤
- 评论列表
-
- 添加评论