How to Compute the Interval List Intersections using Two Pointer

  • 时间：2020-09-16 12:48:17
  • 分类：网络文摘
  • 阅读：103 次

Given two lists of closed intervals, each list of intervals is pairwise disjoint and in sorted order. Return the intersection of these two interval lists.

(Formally, a closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b. The intersection of two closed intervals is a set of real numbers that is either empty, or can be represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].)

Example 1:

merge-intervals How to Compute the Interval List Intersections using Two Pointer Algorithms? algorithms c / c++

merge-intervals

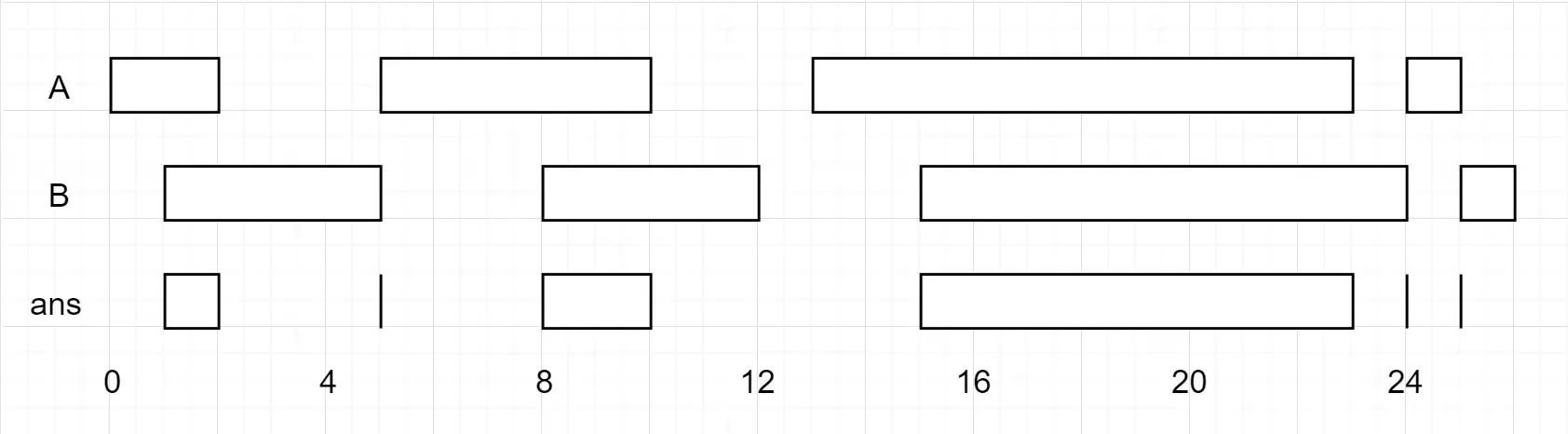
Input: A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
Reminder: The inputs and the desired output are lists of Interval objects, and not arrays or lists.

Note:
0 <= A.length < 1000
0 <= B.length < 1000
0 <= A[i].start, A[i].end, B[i].start, B[i].end < 10^9
NOTE: input types have been changed on April 15, 2019. Please reset to default code definition to get new method signature.

Merge Intervals using Two Pointers

Since the intervals are sorted, we can have two pointers iteratedly incrementing at two sides. There are 3 pairs (6 circumstances) regarding the relations between interval A and B. We then can deal with them accordingly.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

class Solution {
public:
    vector<vector<int>> intervalIntersection(vector<vector<int>>& A, vector<vector<int>>& B) {
        vector<vector<int>> r;
        int n = A.size();
        int m = B.size();
        int i = 0, j = 0;
        while ((i < n) && (j < m)) {
            if (A[i][1] < B[j][0]) {
                i ++;
                continue;
            }
            if (B[j][1] < A[i][0]) {
                j ++;
                continue;
            }
            if ((A[i][0] >= B[j][0]) && (A[i][1] <= B[j][1])) {
                r.push_back(A[i]);
                i ++;
                continue;
            }
            if ((B[j][0] >= A[i][0]) && (B[j][1] <= A[i][1])) {
                r.push_back(B[j]);
                j ++;
                continue;
            }                
            if ((A[i][0] <= B[j][0]) && (A[i][1] <= B[j][1])) {
                r.push_back({B[j][0], A[i][1]});
                i ++;
                continue;
            }
            if ((B[j][0] <= A[i][0]) && (B[j][1] <= A[i][1])) {
                r.push_back({A[i][0], B[j][1]});
                j ++;
                continue;
            }            
        }
        return r;
    }
};
class Solution {
public:
    vector<vector<int>> intervalIntersection(vector<vector<int>>& A, vector<vector<int>>& B) {
        vector<vector<int>> r;
        int n = A.size();
        int m = B.size();
        int i = 0, j = 0;
        while ((i < n) && (j < m)) {
            if (A[i][1] < B[j][0]) {
                i ++;
                continue;
            }
            if (B[j][1] < A[i][0]) {
                j ++;
                continue;
            }
            if ((A[i][0] >= B[j][0]) && (A[i][1] <= B[j][1])) {
                r.push_back(A[i]);
                i ++;
                continue;
            }
            if ((B[j][0] >= A[i][0]) && (B[j][1] <= A[i][1])) {
                r.push_back(B[j]);
                j ++;
                continue;
            }                
            if ((A[i][0] <= B[j][0]) && (A[i][1] <= B[j][1])) {
                r.push_back({B[j][0], A[i][1]});
                i ++;
                continue;
            }
            if ((B[j][0] <= A[i][0]) && (B[j][1] <= A[i][1])) {
                r.push_back({A[i][0], B[j][1]});
                j ++;
                continue;
            }            
        }
        return r;
    }
};

A and B are either: disjoints, inclusive or interleaving.

It could be improved into the following much more concise solution where we calculate the max of the lower bounds and the min of the higher bounds. Then, the interval is pushed if it is valid.

Then we increment the pointer of the interval where it has a smaller upperbound. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution {
public:
    vector<vector<int>> intervalIntersection(vector<vector<int>>& A, vector<vector<int>>& B) {
        vector<vector<int>> r;
        int n = A.size();
        int m = B.size();
        int i = 0, j = 0;
        while ((i < n) && (j < m)) {
            int start = max(A[i][0], B[j][0]);
            int end = min(A[i][1], B[j][1]);
            if (start <= end) {
                r.push_back({start, end});
            }
            if (A[i][1] < B[j][1]) {
                i ++;
            } else {
                j ++;
            }
        }
        return r;
    }
};
class Solution {
public:
    vector<vector<int>> intervalIntersection(vector<vector<int>>& A, vector<vector<int>>& B) {
        vector<vector<int>> r;
        int n = A.size();
        int m = B.size();
        int i = 0, j = 0;
        while ((i < n) && (j < m)) {
            int start = max(A[i][0], B[j][0]);
            int end = min(A[i][1], B[j][1]);
            if (start <= end) {
                r.push_back({start, end});
            }
            if (A[i][1] < B[j][1]) {
                i ++;
            } else {
                j ++;
            }
        }
        return r;
    }
};

Both solutions run in O(M + N) time, and require O(1) constant space (excluding the result vector).

–EOF (The Ultimate Computing & Technology Blog) —

推荐阅读：
劲爆体育直播-劲爆体育在线直播观看「高清」　 辽宁体育直播-辽宁体育在线直播观看「高清」　 北京体育频道直播-北京体育在线直播观看「高清」　 五星体育直播-五星体育在线直播观看「高清」　 风云足球直播-风云足球在线直播观看「高清」　 吉林篮球直播-吉林篮球在线直播观看「高清」　 江苏体育直播-江苏体育在线直播观看「高清」　 广州竞赛直播-广州竞赛频道在线直播观看「高清」　 广东体育频道直播-广东体育频道在线直播观看「高清」　 高尔夫网球频道直播-CCTV高尔夫网球在线直播「高清」　
评论列表
添加评论