Catalan numbers are popular in Combinatoric Mathematics. Many interesting counting problems tend to be solved using the Catalan numbers. The first few Catalan numbers are:

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452

A few interesting Catalan counting problems:

• The number of different ways to cut a convex polygon into triangles i.e. n triangles – Catalan(n) ways
• The number of different ways i.e. Catalan(n) to form a full binary tree with n + 1 leaves
• The number of monotonic lattice paths (which do not pass above the diagonal) along the edges of a grid on a N x N square cells.
• Different ways to generate the parentheses: How to Generate Parentheses using Bruteforce or Depth First Search (Backtracking) Algorithms?

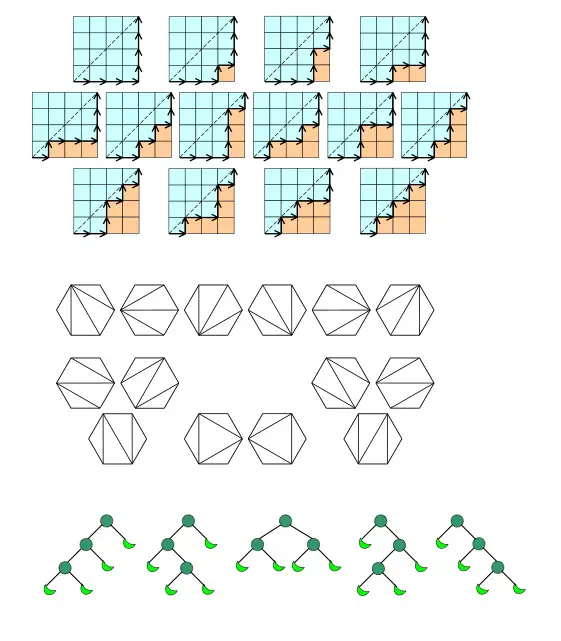
catalan-numbers-applications

Catalan Numbers Math Formula

The Catalan number can be computed in the simple form:

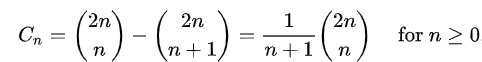
catalan-numbers-formula

There are several ways to compute the nth Catalan number. In order to compute the Catalan numbers in Dynamic Programming, we can use the following recurrence relation:

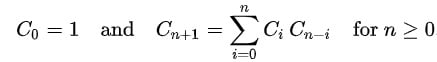
catalan-numbers-recurrence-relations

Alternatively, the following is a simple recurrence relation between Catalan number nth and nth+1.

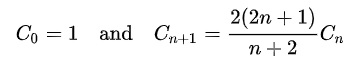
catalan-numbers-recurrence-relations-simple

See this implementation based on the above simple Catalan formula: How to Compute the Catalan Number?

How to Compute the Catalan using Recursions?

The Catalan numbers grow quickly (exponentially) and will overflow if the N is large. The following is a naive implementation of the Catalan formula.

1
2
3
4
5
6
7
8

int64_t catlan(int n) {
    if (n <= 1) return 1;
    int res = 0;
    for (int i = 0; i < n; i ++) {
        res += catlan(i) * catlan(n - i - 1);
    }
    return res;
}

int64_t catlan(int n) {
    if (n <= 1) return 1;
    int res = 0;
    for (int i = 0; i < n; i ++) {
        res += catlan(i) * catlan(n - i - 1);
    }
    return res;
}

However, this implementation is not practically usable as the performance complexity is exponential. The intermediate catalan numbers are computed over and over again.

Dynamic Programming: Computing Catalan Numbers using Recursion + Memoization

We can improve the above recursive implementation into Dynamic Programming by simply using a hash map to store the intermediate calculations e.g. the Memoization.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

unordered_map<int, int64_t> memo;
 
int64_t catlan(int n) {
    if (n <= 1) return 1;
    if (memo.find(n) != memo.end()) {
        // avoid duplicate calculations       
        return memo[n];
    }
    int res = 0;
    for (int i = 0; i < n; i ++) {
        res += catlan(i) * catlan(n - i - 1);
    }
    memo[n] = res; // store into the memo
    return res;
}

unordered_map<int, int64_t> memo;

int64_t catlan(int n) {
    if (n <= 1) return 1;
    if (memo.find(n) != memo.end()) {
        // avoid duplicate calculations       
        return memo[n];
    }
    int res = 0;
    for (int i = 0; i < n; i ++) {
        res += catlan(i) * catlan(n - i - 1);
    }
    memo[n] = res; // store into the memo
    return res;
}

The intermediate calculations are computed and stored into the hash map for later retrieval. The overall time complexity is N square and the space requirement is O(N).

Dynamic Programming: Computing Catalan Numbers using Iterative Approach

Requiring a O(N) vector/array to store the Catalan numbers, we can do this purely iteratively in O(N^2) time complexity. This implementation eliminates the calling stacks due to recursion and is the most efficient (in terms of time and space) among the three implementations presented in this post.

1
2
3
4
5
6
7
8
9
10
11

int catlan(int n) {
    vector<int64_t> dp(n + 1, 0);
    dp[0] = 1;        
    dp[1] = 1;
    for (int i = 2; i <= n; i ++) {
        for (int j = 0; j < i; ++ j) {
            dp[i] += dp[j] * dp[i - j - 1];
        }
    }
    return (int)dp.back();
}

int catlan(int n) {
    vector<int64_t> dp(n + 1, 0);
    dp[0] = 1;        
    dp[1] = 1;
    for (int i = 2; i <= n; i ++) {
        for (int j = 0; j < i; ++ j) {
            dp[i] += dp[j] * dp[i - j - 1];
        }
    }
    return (int)dp.back();
}

You may be interested in this post: How to Compute the Catalan Number?

–EOF (The Ultimate Computing & Technology Blog) —