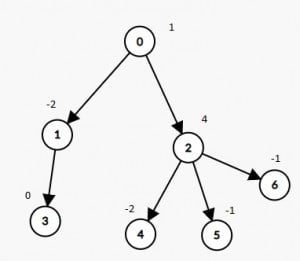
A tree rooted at node 0 is given as follows:

The number of nodes is nodes;
The value of the i-th node is value[i];
The parent of the i-th node is parent[i].
Remove every subtree whose sum of values of nodes is zero.

After doing so, return the number of nodes remaining in the tree.

Input: nodes = 7, parent = [-1,0,0,1,2,2,2], value = [1,-2,4,0,-2,-1,-1]
Output: 2

binary-tree-delete-nodes-with-zero-sum-sub-tree

Constraints:
1 <= nodes <= 10^4
-10^5 <= value[i] <= 10^5
parent.length == nodes
parent[0] == -1 which indicates that 0 is the root.

Hints:
Traverse the tree using depth first search.
Find for every node the sum of values of its sub-tree.
Traverse the tree again from the root and return once you reach a node with zero sum of values in its sub-tree.

How to Delete Nodes from Binary Tree using Depth First Search Algorithm?

The binary tree is given in two arrays, we can convert it using the adjacent graph – two dimension array or vectors. Then we can run a DFS (Depth First Search) algorithm that travels the tree from root to leaves recursively.

Bottom-up, from the leaves, we accumulate the sum and the count of the nodes (remaining). At any point, if the sum is zero, we set the counter to zero – which will be bubbled up as the recursion unrolls.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class Solution {
public:
    int deleteTreeNodes(int nodes, vector<int>& parent, vector<int>& value) {
        vector<vector<int>> g(nodes, vector<int>(0));
        for (int i = 0; i < nodes; ++ i) {
            if (parent[i] == -1) continue;
            g[parent[i]].push_back(i);
        }
        return dfs(g, 0, value)[1];
    }
private:
    vector<int> dfs(const vector<vector<int>> &g, int root, const vector<int>& value) {
        int sum = value[root];
        int remain = 1;
        for (const auto &child: g[root]) {
            vector<int> r = dfs(g, child, value);
            remain += r[1];
            sum += r[0];
        }
        if (sum == 0) remain = 0;
        return {sum, remain};
    }
};

class Solution {
public:
    int deleteTreeNodes(int nodes, vector<int>& parent, vector<int>& value) {
        vector<vector<int>> g(nodes, vector<int>(0));
        for (int i = 0; i < nodes; ++ i) {
            if (parent[i] == -1) continue;
            g[parent[i]].push_back(i);
        }
        return dfs(g, 0, value)[1];
    }
private:
    vector<int> dfs(const vector<vector<int>> &g, int root, const vector<int>& value) {
        int sum = value[root];
        int remain = 1;
        for (const auto &child: g[root]) {
            vector<int> r = dfs(g, child, value);
            remain += r[1];
            sum += r[0];
        }
        if (sum == 0) remain = 0;
        return {sum, remain};
    }
};

The time complexity is O(N) where N is the number of the nodes in the binary tree. The space complexity is also O(N) due to the stack in recursion.

–EOF (The Ultimate Computing & Technology Blog) —