Depth First Search Algorithm to Compute the Smallest String Star

  • 时间：2020-09-09 13:16:32
  • 分类：网络文摘
  • 阅读：109 次

Given the root of a binary tree, each node has a value from 0 to 25 representing the letters ‘a’ to ‘z’: a value of 0 represents ‘a’, a value of 1 represents ‘b’, and so on.

Find the lexicographically smallest string that starts at a leaf of this tree and ends at the root.

(As a reminder, any shorter prefix of a string is lexicographically smaller: for example, “ab” is lexicographically smaller than “aba”. A leaf of a node is a node that has no children.)

Example 1:
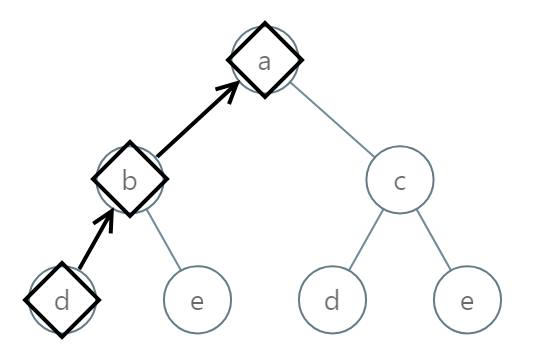
Input: [0,1,2,3,4,3,4]
Output: “dba”
binary-tree1 Depth First Search Algorithm to Compute the Smallest String Starting From Leaf algorithms c / c++ DFS recursive

Example 2:
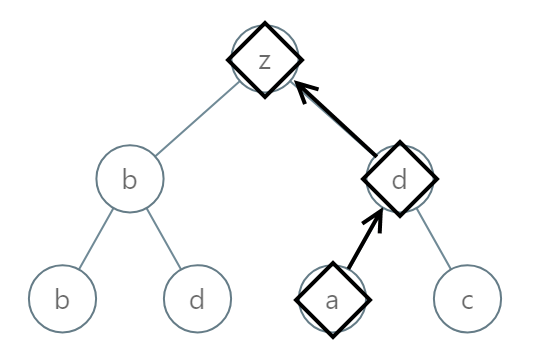
Input: [25,1,3,1,3,0,2]
Output: “adz”
binary-tree2 Depth First Search Algorithm to Compute the Smallest String Starting From Leaf algorithms c / c++ DFS recursive

Example 3:
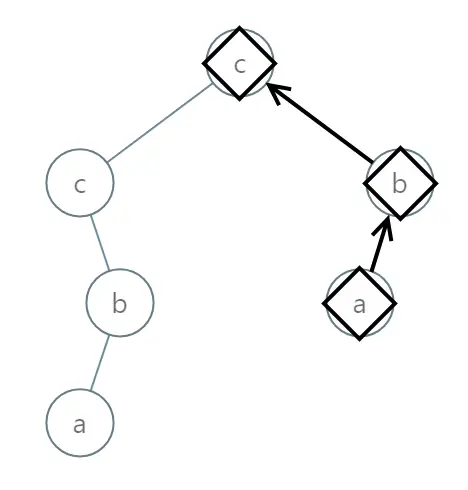
Input: [2,2,1,null,1,0,null,0]
Output: “abc”
binary-tree3 Depth First Search Algorithm to Compute the Smallest String Starting From Leaf algorithms c / c++ DFS recursive

Note:
The number of nodes in the given tree will be between 1 and 8500.
Each node in the tree will have a value between 0 and 25.

Recursive Depth First Search to Compute the Smallest String Starting From Leaf

We can start from the Root, perform a recursive DFS (Depth First Search) algorithm, and pass the string along down to the leaves. When we reach a leaf node, we construct the final string, and store the smallest one (alphabetically).

All nodes are visisted exactly once. When we finish searching the tree, we have the answer. The time complexity is O(N). In this particular case, the DFS is also the bruteforce algorithm.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    string smallestFromLeaf(TreeNode* root) {
        dfs(root, "");
        return ans;
    }
private:
    string ans = "";
    void dfs(TreeNode* root, string cur) {
        if (!root) return;
        if ((root->left == nullptr) && (root->right == nullptr)) {
            cur = (char)(97 + root->val) + cur;
            if ((ans == "") || (cur < ans)) {
               ans = cur; 
            }
            return;
        }
        dfs(root->left, (char)(97 + root->val) + cur);
        dfs(root->right,(char)(97 + root->val) + cur);
    }
};
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    string smallestFromLeaf(TreeNode* root) {
        dfs(root, "");
        return ans;
    }
private:
    string ans = "";
    void dfs(TreeNode* root, string cur) {
        if (!root) return;
        if ((root->left == nullptr) && (root->right == nullptr)) {
            cur = (char)(97 + root->val) + cur;
            if ((ans == "") || (cur < ans)) {
               ans = cur; 
            }
            return;
        }
        dfs(root->left, (char)(97 + root->val) + cur);
        dfs(root->right,(char)(97 + root->val) + cur);
    }
};

Depth First Searching Algorithm using Stack

The Recursion uses implicit stacks. The compiler generates the calling stacks. The recursion code usually is more clean and concise. We can also use a stack to manually emulate the recursive calls.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    string smallestFromLeaf(TreeNode* root) {
        if (!root) return "";
        stack<pair<TreeNode*, string>> st;
        st.push({root, ""});
        string ans = "";
        while (!st.empty()) {
            auto p = st.top();
            st.pop();
            if (p.first->right) {
                st.push({p.first->right, (char)(97 + p.first->val) + p.second});
            }            
            if (p.first->left) {
                st.push({p.first->left, (char)(97 + p.first->val) + p.second});
            }
            if ((p.first->left == nullptr) && (p.first->right == nullptr)) {
                string v = (char)(97 + p.first->val) + p.second;
                if ((ans == "") || (v < ans)) {
                    ans = v;   
                }                
            }
        }
        return ans;
    }
};
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    string smallestFromLeaf(TreeNode* root) {
        if (!root) return "";
        stack<pair<TreeNode*, string>> st;
        st.push({root, ""});
        string ans = "";
        while (!st.empty()) {
            auto p = st.top();
            st.pop();
            if (p.first->right) {
                st.push({p.first->right, (char)(97 + p.first->val) + p.second});
            }            
            if (p.first->left) {
                st.push({p.first->left, (char)(97 + p.first->val) + p.second});
            }
            if ((p.first->left == nullptr) && (p.first->right == nullptr)) {
                string v = (char)(97 + p.first->val) + p.second;
                if ((ans == "") || (v < ans)) {
                    ans = v;   
                }                
            }
        }
        return ans;
    }
};

During the code interviews, if you are asked this question, it is better to go with the Recursion. But you can follow up with the non-recursive/iterative approach.

–EOF (The Ultimate Computing & Technology Blog) —

推荐阅读：
冰淇淋为何要加如此多的食品添加剂　 肉禽类的这些部位千万不要去吃　 百事可乐配方含致癌色素仍坚称安全　 调查称槟榔是一级致癌物可引发口腔癌　 嚼食槟榔对身体健康的危害非常大　 槟榔被认定为一级致癌物可引发口腔癌　 食品安全监管工作的有效性令人疑惑　 厂家称没法根本解决五芳斋粽子发霉　 饮食保健：盘点枸杞的十大养生功效　 食物为何会致癌及常见致癌物来源　
评论列表
添加评论