The Union Find (Disjoint Set) Implementation in Java/C++

  • 时间：2020-09-07 12:03:44
  • 分类：网络文摘
  • 阅读：151 次
2091E060-120E-4C44-BAA3-7E4E0DF7BD55 The Union Find (Disjoint Set) Implementation in Java/C++ algorithms c / c++ implementation java

Java

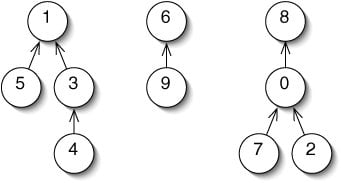
The Union-Find (Disjoint Set) is a commonly-used algorithm that can solve e.g. Minimal Spanning Tree. The following is a Java implementation of a Union-Find Class.

disjoint1 The Union Find (Disjoint Set) Implementation in Java/C++ algorithms c / c++ implementation java 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

package com.helloacm;
 
public class UnionFind {
    private int[] parent;
    public UnionFind(int n) {
        parent = new int[n];
        for (var i = 0; i < n; i++) {
            parent[i] = i;
        }
    }
 
    public int Find(int x) {
        if (x == parent[x]) {
            return x;
        }
        // compress the paths
        return parent[x] = Find(parent[x]);
    }
 
    public void Union(int x, int y)  {
        var px = Find(x);
        var py = Find(y);
        if (px != py) {
            parent[px] = py;
        }
    }
}
package com.helloacm;

public class UnionFind {
    private int[] parent;
    public UnionFind(int n) {
        parent = new int[n];
        for (var i = 0; i < n; i++) {
            parent[i] = i;
        }
    }

    public int Find(int x) {
        if (x == parent[x]) {
            return x;
        }
        // compress the paths
        return parent[x] = Find(parent[x]);
    }

    public void Union(int x, int y)  {
        var px = Find(x);
        var py = Find(y);
        if (px != py) {
            parent[px] = py;
        }
    }
}

The above algorithm uses O(N) space and requires O(N) time. Example usage:

1
2
3
4
5
6
7
8
9
10

package com.helloacm;
 
public class Main {
    public static void main(String[] args) {
        var uf = new UnionFind(5);
        System.out.println(uf.Find(3));
        uf.Union(3, 4);
        System.out.println(uf.Find(3)); // after join, 3's parent is 4.
    }
}
package com.helloacm;

public class Main {
    public static void main(String[] args) {
        var uf = new UnionFind(5);
        System.out.println(uf.Find(3));
        uf.Union(3, 4);
        System.out.println(uf.Find(3)); // after join, 3's parent is 4.
    }
}

This Java code prints 3 and 4.

C++ Disjoint Set / Union Find Algorithm Implementation

Similar, here is the C++ implementation of the Disjoint Set data structure. The union is a keyword in C++ and therefore we implement Union method instead:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class UF {
    public:
        UF(int N) {
            G.resize(N);
            std::iota(begin(G), end(G), 0);
        }
    
        int Find(int x) {
            if (x == G[x]) {
                return x;
            }
            return G[x] = Find(G[x]);
        }
    
        void Union(int x, int y) {
            int px = Find(x);
            int py = Find(y);
            if (px != py) {
                G[px] = py;    
            }            
        }    
    private:
        vector<int> G;
};
class UF {
    public:
        UF(int N) {
            G.resize(N);
            std::iota(begin(G), end(G), 0);
        }
    
        int Find(int x) {
            if (x == G[x]) {
                return x;
            }
            return G[x] = Find(G[x]);
        }
    
        void Union(int x, int y) {
            int px = Find(x);
            int py = Find(y);
            if (px != py) {
                G[px] = py;    
            }            
        }    
    private:
        vector<int> G;
};

Here, we use the iota from STL to easily assign incrementing values to the initial Group vector:

1
2

// G = {0, 1, 2, ...};
std::iota(begin(G), end(G), 0);
// G = {0, 1, 2, ...};
std::iota(begin(G), end(G), 0);

Compress Paths and Union Rules for Disjoint Set

As shown above - when in Find - we can compress the paths. Also, in the Union, we can either set G[px] = py or G[py] = px.

Choose a smaller group ID

This would be easiest - we compare the px and py value before setting the group:

1
2
3
4
5
6
7
8

void Union(int x, int y) {
  int px = Find(x);
  int py = Find(y);
  if (px != py) {
    if (px < py) swap(px, py); // make py smaller
    G[px] = py;    
  }            
} 
void Union(int x, int y) {
  int px = Find(x);
  int py = Find(y);
  if (px != py) {
    if (px < py) swap(px, py); // make py smaller
    G[px] = py;    
  }            
}

Merging into Smaller Size

Alternatively, we can allocate an addition array to store the sizes for each group and always merge the larger group into the smaller one:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class UF {
    public:
        UF(int N) {
            G.resize(N);
            std::iota(begin(G), end(G), 0);
            sizes.resize(N);
            std::fill(begin(sizes), end(sizes), 1);
        }
    
        int Find(int x) {
            if (x == G[x]) {
                return x;
            }
            return G[x] = Find(G[x]);
        }
    
        void Union(int x, int y) {
            int px = Find(x);
            int py = Find(y);
            if (px != py) {
                if (sizes[px] < sizes[py]) swap(px, py);
                G[px] = py;    
                sizes[py] += sizes[px];
            }            
        }    
    private:
        vector<int> G;
        vector<int> sizes;
};
class UF {
    public:
        UF(int N) {
            G.resize(N);
            std::iota(begin(G), end(G), 0);
            sizes.resize(N);
            std::fill(begin(sizes), end(sizes), 1);
        }
    
        int Find(int x) {
            if (x == G[x]) {
                return x;
            }
            return G[x] = Find(G[x]);
        }
    
        void Union(int x, int y) {
            int px = Find(x);
            int py = Find(y);
            if (px != py) {
                if (sizes[px] < sizes[py]) swap(px, py);
                G[px] = py;    
                sizes[py] += sizes[px];
            }            
        }    
    private:
        vector<int> G;
        vector<int> sizes;
};

--EOF (The Ultimate Computing & Technology Blog) --

推荐阅读：
劲爆体育直播-劲爆体育在线直播观看「高清」　 辽宁体育直播-辽宁体育在线直播观看「高清」　 北京体育频道直播-北京体育在线直播观看「高清」　 五星体育直播-五星体育在线直播观看「高清」　 风云足球直播-风云足球在线直播观看「高清」　 吉林篮球直播-吉林篮球在线直播观看「高清」　 江苏体育直播-江苏体育在线直播观看「高清」　 广州竞赛直播-广州竞赛频道在线直播观看「高清」　 广东体育频道直播-广东体育频道在线直播观看「高清」　 高尔夫网球频道直播-CCTV高尔夫网球在线直播「高清」　
评论列表
添加评论